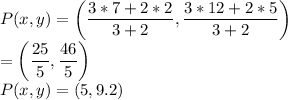Question

What is the coordinate of point P that lies along the directed line segment from Q(2, 5) to R(7, 12) and partitions the segment in the ratio of 3 to 2? (3, 4.2) (4.5, 8.5) (5, 9.2) (5, 7)

Answer 1

(C)(5,9.2)

Explanation:

Given points Q(2, 5) and R(7, 12). We are to determine the coordinate of point P that lies along the directed line segment which partitions the segment in the ratio of 3 to 2.

For internal division of a line segment, the coordinate of the point which partitions the segment in the ratio m:n is given as:

`\left((mx_2+nx_1)/(m+n) , (my_2+ny_1)/(m+n)\right)`

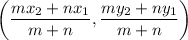
m:n =3:2

`(x_1,y_1)=Q(2,5)\\(x_2,y_2)=R(7,12)`

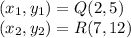
Therefore:

`P(x,y)=\left((3*7+2*2)/(3+2) , (3*12+2*5)/(3+2)\right)\\=\left((25)/(5) , (46)/(5)\right)\\P(x,y)=(5,9.2)`