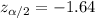Answer:
The signficance level is 0.05 and then based in the alternative hypothesis we can find a critical value who accumulates 0.05 of the area in the normal standard curve in the left and we got:
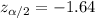
Explanation:
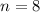 the same size given
the same size given
[te]\sigma[/tex] the population deviation is known
For this case we want to test if the population mean is less than 15 and that represent the alternative hypothesis and the complement would be the null hypothesis. So then the system of hypothesis are:
Null hypothesis:
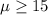
Alternative hypothesis:

The signficance level is 0.05 and then based in the alternative hypothesis we can find a critical value who accumulates 0.05 of the area in the normal standard curve in the left and we got: