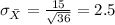Question

Random samples of size 36 are taken from a process (an infinite population) whose mean and standard deviation are 20 and 15, respectively. The distribution of the population is unknown. The mean and the standard error of the distribution of sample mean are _____.

Answer 1

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

The mean is given by:

`\mu_(\bar X)= 20`

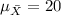
And the standard error would be:

`\sigma_(\bar X) =(15)/(√(36))= 2.5`

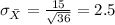
Explanation:

We have the following info given:

`n =36` represent the random samples taken from an infinite population

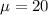`\mu = 20` represent the mean

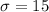`\sigma =15` represent the standard deviation

Since we don't know the distribution but we know that the sample size is large enough (n>30) in order to apply the central limit theorem and for this case the sample mean have the following distribution:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

The mean is given by:

`\mu_(\bar X)= 20`

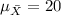
And the standard error would be:

`\sigma_(\bar X) =(15)/(√(36))= 2.5`