Question

Prices to a concert cost N$200 for an adult and N$150 for a child, the concert venue can accommodate at most 240 people. The organizers are giving a N$20 discount to every adult and N$10 discount for every child but do not want the total discounted amount to exceed N$3200. Draw a graph and use it to answer the following questions: i. How many tickets altogether should the organisers sell in order to maximise their sales amount? ii. How many tickets of each type (adult and child) should they sell to get a maximum sales amount? iii. What is the maximum sales amount the organisers can make? iv. If the profit is calculated as follows: profit = total sales – total discount amount. How much profit will the organisers make from the maximum sales? Overall presentation (neat, clear and well presented)

Answer 1

i. 240 tickets

ii. 80 adults and 160 children

iii. N$ 40,000.00

iv. Profit= N$ 36,800.00

Step-by-step explanation:

Ok so in order to solve this problem we need to start by building our system of equations from the restrictions the problem gives us:

let's say that

x=# of adult tickets

y= # of children tickets

so

"... the concert venue can accommodate at most 240 people."

this translates to the following inequality:

`x+y\leq240`

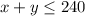
"The organizeres are giving a N$20 discount to every adult and N$10 discount for every child but do not want the total descounted amount to exceed N$3200."

Translates to

`20x+10y\leq3200`

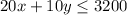
and we know we cannot sell a negative number of adult and children tickets so the last restrictions are:

`x\geq0`

`y\geq0`

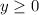
so we can now graph our system of inequalities (see graph attached)

the procedure to graph a linear equation is as follows:

1. Pick an x-value

2. Find the corresponding y-value with the provided equation we need to graph.

3. Write the coordinates as an ordered pair (x,y)

4. Repeat the process with a second x-value.

5. Graph the two points you found on the previous steps.

6. Connect the points with a straight line.

So the feasible region is the one that all restrictions will have in common and the maximum and minimum points for our objective function will be the marked points, which are the vertices of the feasible region. So we test them to see which will maximize our objective function.

Objective function:

s=200x+150y

(0,0)

s=200(0)+150(0)=0

(0,240)

s=200(0)+150(240)=N$36,000

(80,160)

s=200(80)+150(160)=N$40,000

(160,0)

s=200(160)+150(0)=N$32,000

So when comparing the results we can see that the objective function will be maximized at the point (80,160) so:

i) How many tickets altogether should the organisers sell in order to maximize their sales amount?

total # of tickets = x+y = 80+160=240 tickets

ii) How many tickets of each type (adult and child) should they sell to get a maximum sales amount?

x y

80 adult tickets and 160 child tickets.

iii) What is the maximum sales amount the organizers can make?

s=200(80)+150(160)=N$40,000

iv) If the profit is calculated as follows: profit = total sales - total discount amount. How much profit will the organisers make from the maximum sales?

Profit= total sales - total discount

total sales=200(80)+150(160)=N$40,000

total discount = 20(80)+10(160)=N$3,200

Profit=N$40,000-N$3,200=N$36,800.00