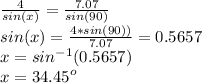Question

The diagrams shows a 3cm x 5cm x 4cm cuboid.

Answer 1

a) 5.83 cm

b) 34.45°

Explanation:

a) From Pythagoras theorem of right triangles, given right triangle ABC:

AB² + BC² = AC²

Therefore:

AC² = 5² + 3²

AC² = 25 + 9 = 34

AC = √34

AC = 5.83 cm

b) From triangle ACD, AC = 5.83 cm, AD = 4 cm and ∠A = 90°.

From Pythagoras theorem of right triangles, given right triangle ACD:

AD² + AC² = DC²

Therefore:

DC² = 5.83² + 4²

DC² = 34 + 16 = 50

DC = √50

DC = 7.07 cm

Let ∠ACD be x. Therefore using sine rule:

`(4)/(sin(x))=(7.07)/(sin(90)) \\ sin(x)=(4*sin(90)))/(7.07)=0.5657\\ x=sin^(-1)(0.5657)\\x=34.45^o`