Question

Which graph shows the solution to the equation below? log Subscript 3 Baseline (x + 3) = log Subscript 0.3 (x minus 1) On a coordinate plane, 2 curves intersect at (1, 1). One curve curves up and to the right from quadrant 3 into quadrant 1. The other curve curves down from quadrant 1 into quadrant 4. On a coordinate plane, 2 identical curves are shown. One curve starts at y = negative 3, and the other curve starts at y = 1. On a coordinate plane, a curve and a line are shown. On a coordinate plane, a curve and a cubic function are shown. Mark this and return

Answer 1

A on edge2020

Explanation:

took the test

Answer 2

On a coordinate plane, 2 curves intersect at (1, 1). One curve curves up and to the right from quadrant 3 into quadrant 1. The other curve curves down from quadrant 1 into quadrant 4

Explanation:

The first function is given as:

`log_3(x+3)`

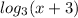
The second function is given as:

`log_(0.3)(x-1)`

First we graph both the functions.

We can see that one curves up and to the right from quadrant 3 into quadrant 1. This curve is of
`log_3(x+3)`

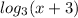
The other curve curves down from quadrant 1 into quadrant 3

Both curves interest almost at (1,1)

See the graph attached below

Blue line represents first function

Green line represents second function

The solution lies on the Red line.