Answer:
2250m
Explanation:
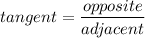
We have:
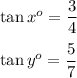
By definition of tangent, we have:
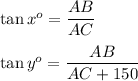
Therefore we have the system of equations:
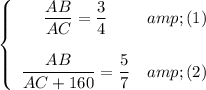
From (1)
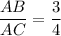 cross multiply
cross multiply
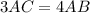 divide both sides by 3
divide both sides by 3
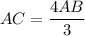
Substitute it to (2):
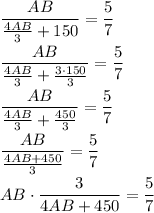
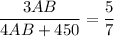 cross multiply
cross multiply
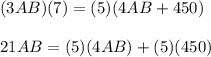
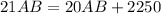 subtract 20AB from both sides
subtract 20AB from both sides
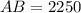
Such a tower height is rather impossible, but this is the solution.