Question

The incorrect work of a student to solve an equation 2(y + 6) = 4y is shown below.

Step 1: 2(y + 6) - 4y
Step 2: 2y + 8; 4y
Step 3: 2y : 8
Step 4: y = 4
Which of the following explains how to correct Step 2 and shows the correct value of y?
02 should be distributed as 2y + 12, y = 6
should be distributed as 2y + 12; y = 3
The equation should be y + 6 4y after division by 2
D The equation should De
6 = 4y after division by 2; y = 1

Answer 1

⇒ A. 2 should be distributed as 2y + 12, y = 6

Explanation:

Here are the steps to solve this equation:

Given:

First step: 2(y+6)-4y

Use the distributive property.

Distributive property:

⇒ A(B+C)=AB+AC

2(y+6)

2*y=2y

2*6=12

2y+12

Isolate the term of y from one side of the equations.

2y+12=4y

Subtract by 12 from both sides.

2y+12-12=4y-12

Solve.

2y=4y-12

Then, you subtract by 4y from both sides.

2y-4y=4y-12-4y

Solve.

2y-4y=-2y

-2y=-12

Divide by -2 from both sides.

`\sf{(-2y)/(-2)=(-12)/(-2)}`

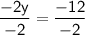
Solve.

Divide the numbers from left to right.

Solutions:

-12/-2=6

`\Longrightarrow: \boxed{\sf{y=6}}`

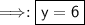
• Therefore, the correct answer is A. "2 should be distributed as 2y+12, y=6".

I hope this helps. Let me know if you have any questions.