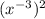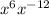Answer:
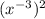
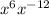
Explanation:
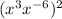 is the expression given to be solved.
is the expression given to be solved.
First of all let us have a look at 3 formulas:
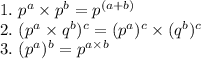
Both the formula can be applied to the expression(
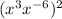 ) during the first step while solving it.
) during the first step while solving it.
Applying formula (1):
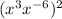
Comparing the terms of
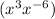 with
with
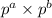
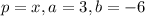
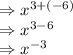
So,
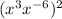 is reduced to
is reduced to
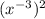
Applying formula (2):
Comparing the terms of
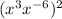 with
with
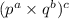
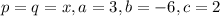
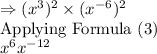
So,
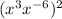 is reduced to
is reduced to
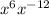 .
.
So, the answers can be: