Question

The congressional committees on mathematics and computer science are made up of five representatives each, and a congressional rule is that the two committees must be disjoint. If there are 385 members of congress, how many ways could the committees be selected?

Answer 1

The committes can be selected in
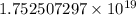`1.752507297 * 10^(19)` ways

Explanation:

The order in which the members are chosen to the committee is not important. So we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

The two committees must be disjoint.

This means that a person cannot be part of both committes.

If there are 385 members of congress, how many ways could the committees be selected?

Since the committes are disjoint, 5(math) + 5(computer science) = 10 people will be chosen from the set of 385. So

`C_(385,10) = (385!)/(10!(385-10)!) = 1.752507297 * 10^(19)`

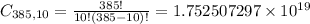
The committes can be selected in
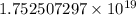`1.752507297 * 10^(19)` ways