Question

A piston-cylinder assembly contains 5kg of water that undergoes a series of processes to form a thermodynamic cycle. Process 1à2: Constant pressure cooling from p1=20bar and T1=360°C to saturated vapor Process 2à3: Constant volume cooling to p3=5 bar Process 3à4: Constant pressure heating Process 4à1: Polytropic process following Pv =constant back to the initial state Kinetic and potential energy effects are negligible. Calculate the net work for the cycle in kJ.

Answer 1

The net work done is 272.38 kJ

Step-by-step explanation:

The parameters given are;

Mass of water = 5 kg

p₁ = 20 bar

T₁ = 360°C

v₁ = 0.141147 m³/kg

Process 1 to 2 = Constant pressure process

p₂ = 20 bar

Process 2 to 3 = Constant volume process

p₃ = 5 bar

Process 3 to 4 = Constant pressure process

Process 4 to 1 = Polytropic process pv = Constant

For Stage 1 to 2, we have;

p₂ = 20 bar

From the steam tables for superheated steam, we have;

T₂ = 212.385°C

v₂ = 0.0995805 m³/kg

Work done = p₂×(v₂ - v₁) = 2×10⁶ × (0.0995805 - 0.141147 ) = -83133 J/kg

For the 5 kg, we have;

`W_(1-2)` = -83133 J/kg × 5 = -415,665 J

Stage 2 to 3: Constant volume cooling

v₂ = v₃ = 0.0995805 m³/kg

p₃ = 5 bar

T₃ = 151.836°C

(0.0995805 - 0.00109256)/(0.374804 - 0.00109256) = 0.2635 liquid vapor mixture

Work done,
`W_(2-3)` = 0

Stage 3 to 4: Constant pressure heating

p₃ = p₄ = 5 bar

v₄/T₄ = v₃/T₃

v₄ = 0.374804 m³/kg

T₄ = v₄×T₃/v₃ = 0.374804*(273.15 + 151.836)/0.0995805 = 1599.6 K = 1326.4 °C

Work done = p₄×(v₄ - v₃) = 5×10⁵ × (0.374804 - 0.0995805 ) = 137611.75 J/kg

For the 5 kg, we have;

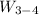`W_(3-4)` = 137,611.75 J/kg × 5 = 688,058.75 J

Stage 4 to 1: Polytropic process

`(p_(4))/(p_(1)) = \left ((V_(1))/(V_(4)) \right )^(n) = \left ((T_(4))/(T_(1)) \right )^{(n)/(n-1)}`

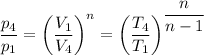
Which gives;

`(5)/(20) = \left ((0.141147 )/(0.374804) \right )^(n)`

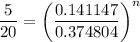
n = log(5/20) ÷log(0.141147/0.374804) = 1.42

Work done,
`W_(pdv)`, is given as follows;

`W_(pdv) = (p_4 * v_4 -p_4 * v_4 )/(n-1)`

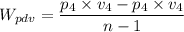
Which gives;

`W_(pdv) = (5* 0.374804 -20* 0.141147 )/(1.42-1) = -2.259 \, J`

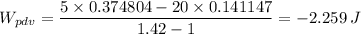
For the 5 kg, we have;

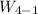`W_(4-1)` = -2.259 J/kg × 5 = -11.2967 J

The net work done,
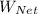`W_(Net)`, is therefore;

`W_(Net)` =
`W_(1-2)` +
`W_(3-4)` +
`W_(4-1)`

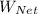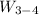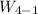
-415,665 + 688,058.75 -11.2967 = 272,382.45 J = 272.38 kJ.