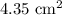Question

9. What is the area of the region left if three equilateral triangles are cut off

from a semi circle of radius 4cm? *​

Answer 1

`4.35$ cm^2`

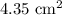
Explanation:

For the equilateral triangle in a semicircle of radius 4cm.

Side Lengths =4cm

Angles =60 degrees

`\text{Area of a Triangle}=(1)/(2)ab\sin \theta`

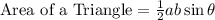
Therefore, the area of one equilateral triangle

`=(1)/(2)*4*4*\sin 60^\circ`

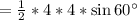
Area of the three equilateral triangle

`=3*(1)/(2)*4*4*\sin 60^\circ\\=20.7846$ cm^2`

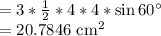
Area of the semicircle

`=0.5 * \pir^2\\=0.5 * \pi * 4^2\\=25.1327$ cm^2`

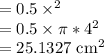
Therefore, the area left over =Area of Semicircle -Area of Triangles

=25.1327-20.7846

=
`4.35$ cm^2`