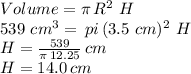Question

Plz solve this question .

the volume of cylindrical object 539cm
and the circumference of the base of
the cylinder is 22 cm.find its height.

Answer 1

The cylinder's height is 14 cm

Explanation:

Recall that the formula for the volume of a cylinder is given by:

`Volume=\pi\,R^2\,\,H`

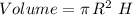
where R is the radius of the cylinder's base, and H the cylinder's height (which we we don't know and need to find)

In order to use this formula to solve for our unknown we need to obtain the radius "R" by using the second piece of information on the length of the base's circumference (22 cm). Recall the formula for the length of a circumference of radius R:

`length=2\,\pi\,\,R`

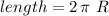
Then, in our case:

`length=2\,\pi\,\,R\\22=2\,\pi\,\,R\\R=(22)/(2\,\pi) \\R=3.50\,\,cm`

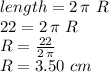
We now use this information in the volume equation to find the cylinder's height:

`Volume=\pi\,R^2\,\,H\\539\,\,cm^3=\,pi\,(3.5\,\,cm)^2\,\,H\\H=(539)/(\pi\,12.25) \,cm\\H=14.0 \,cm`