Question

Use the following information for questions 8-10: A professional basketball player has an 81% success rate when shooting free throws. Let the random variable X represent the number of free throws he makes in a random sample of 10 free throws (assume this experiment meets all binomial requirements). What is the expected number of free throws he will make

Answer 1

The expected number of free throws he will make is 8.1.

Explanation:

For each free throw, there are only two possible outcomes. Either he makes it, or he misses each. Each free throw is independent of other free throws. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

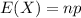
A professional basketball player has an 81% success rate when shooting free throws.

This means that
`p = 0.81`

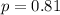
Sample of 10 free throws

This means that
`n = 10`

What is the expected number of free throws he will make

`E(X) = np = 10*0.81 = 8.1`

The expected number of free throws he will make is 8.1.