Question

A CD has a mass of 16.0 g and a radius of 6.03 cm. When inserted into a player, the CD starts from rest and accelerates to an angular velocity of 19.5 rad/s in 0.685 s. Assuming the CD is a uniform solid disk, determine the net torque acting on it

Answer 1

The net torque acting on the CD is
`8.281* 10^(-4)\,N\cdot m`.

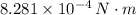Step-by-step explanation:

According to the D'Alembert's Principle, net torque of a rigid body is equal to the product of the moment of inertia with respect to its center of gravity and angular acceleration. That is:

`\tau = I_(g)\cdot \alpha`

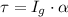
Where:

`\tau` - Net torque, measured in Newton-meters.

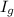`I_(g)` - Moment of inertia, measured in kilogram-square meters.

`\alpha` - Angular acceleration, measured in radians per square second.

The moment of inertia of a solid disk is:

`I_(g) = (1)/(2)\cdot m \cdot r^(2)`

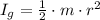
Given that
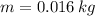`m = 0.016\,kg` and
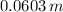`0.0603\,m`, the moment of inertia of the CD is:

`I_(g) = (1)/(2)\cdot (0.016\,kg)\cdot (0.0603\,m)^(2)`

`I_(g) = 2.909* 10^(-5)\,kg\cdot m^(2)`

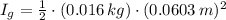
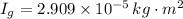
Let suppose that CD accelerates constantly, so that motion equation is the following:

`\omega = \omega_(o) + \alpha \cdot t`

`\alpha = (\omega - \omega_(o))/(t)`

`\alpha = (19.5\,(rad)/(s)-0\,(rad)/(s) )/(0.685\,s)`

`\alpha = 28.467\,(rad)/(s^(2))`

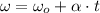
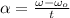
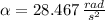
Finally, the net torque acting on the CD is:

`\tau = (2.909* 10^(-5)\,kg\cdot m^(2))\cdot \left(28.467\,(rad)/(s^(2))\right)`

`\tau = 8.281* 10^(-4)\,N\cdot m`

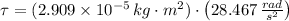
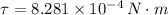
The net torque acting on the CD is
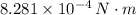`8.281* 10^(-4)\,N\cdot m`.