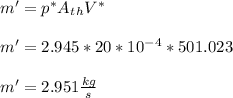Answer:
a) P* = 0.5283 MPa , T* = 624.75 K , ρ* = 2.945 kg/m^3 , V* = 501.023 m/s
b) Pe = 0.1278 MPa , Te = 416.7 K , ρe = 1.069 kg/m^3 , Ve = 818.36 m/s, Ae = 33.75 cm^2
c) m' = 2.915 kg/s
Step-by-step explanation:
Given:-
- The inlet pressure, Pi = 1.0 MPa
- The inlet temperature, Ti = 750 K
- Inlet velocity is negligible
- Steady, Isentropic Flow
- The specific heat ratio of air, k = 1.4
- Exit Mach number, Mae = 2
- The throat area, Ath = 20 cm^2
- Gas constant of air, R = 0.287 KJ / kg.K
Find:-
(a) the throat conditions (static pressure, temperature, density, and mach number)
b) the exit plane conditions
c) the mass flow rate
Solution:-
- For this problem we will assume air to behave like an ideal gas with constant specific heat at RTP. Also the flow of air through the nozzle is assumed to be steady, one dimensional, and Isentropic with constant specific heat ratio ( k ).
- First we will scrutinize on the exit conditions. We have a Mach number of 2 at the exit. The flow at the exit of converging-diverging nozzle is in super-sonic region this is only possible only if sonic ( Ma = 1 ) conditions are achieved by the flow at the throat area ( minimum cross-sectional area ).
- Moreover, the flow is almost still at the inlet. Hence, we can assume that the flow has negligible velocity ( vi = 0 m/s ) at the inlet and the reservoir temperature and pressure can be assumed to be stagnation temperature and pressures as follows:

- Using the ideal gas law we can determine the stagnation density ( ρo ) as follows:
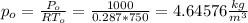
- We will use the already developed results for flow which has reached sonic velocity ( Ma = 1 ) at the throat region. Use Table A - 13, to determine the critical static values at the throat region:

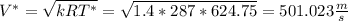
- Similarly, we will again employ the table A - 13 to determine the exit plane conditions for ( Ma = 2 ) as follows:

- The velocity at the exit plane ( Ve ) can be determined from the exit conditions as follows:
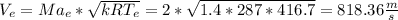
- For steady flows the mass flow rate ( m' ) is constant at any section of the nozzle. We will use the properties at the throat section to determine the mass flow rate as follows: