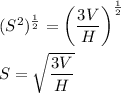Question

Question one answer: S²=3V/H

What is the opposite operation of squaring? Using this opposite operation, rewrite the equation from question 1 so s is by itself on one side of the equation.


Step by step answer

Answer 1

`\ S=\sqrt{(3V)/(H)}}`

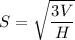
Explanation:

The opposite operation of squaring is taking the square root.

`\ S=\sqrt{(3V)/(H)}}`

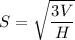
We know that the denominator of a fractional power is the index of the corresponding root:

`\displaystyle x^(1)/(n)=\sqrt[n]{x}`

For n=2, we don't usually write the index in the root symbol:

`x^{(1)/(2)}=√(x)`

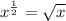
In the case of this problem, ...

`(S^2)^{(1)/(2)}=\left((3V)/(H)\right)^{(1)/(2)}\\\\S=\sqrt{(3V)/(H)}`