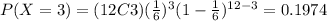Question

Question 6

An experiment consists of rolling a single die 12 times and the variablex is the number of times that the outcome is 6. Use binomial distribution to find the probability that the


outcome of 6 occurs exactly 3 times

Answer 1

`P(X=3)`

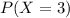
And using the probability mass function we got:

`P(X=3)= (12C3)((1)/(6))^3 (1-(1)/(6))^(12-3)=0.1974`

Explanation:

Let X the random variable of interest "number of times that 6 appears", on this case we now that:

`X \sim Binom(n=12, p=1/6)`

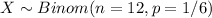
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

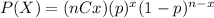
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

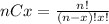
And we want to find this probability:

`P(X=3)`

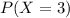
And using the probability mass function we got:

`P(X=3)= (12C3)((1)/(6))^3 (1-(1)/(6))^(12-3)=0.1974`