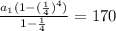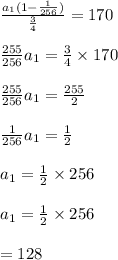Question

The common ratio of a geometric series is \dfrac14 4 1 ​ start fraction, 1, divided by, 4, end fraction and the sum of the first 444 terms is 170170170.

Answer 1

The first term is 128

Answer 2

The common ratio of a geometric series is \dfrac14

4

1 ​

start fraction, 1, divided by, 4, end fraction and the sum of the first 4 terms is 170

The first term is 128

Explanation:

The common ratio of the geometric series is given as:

`r = (1)/(4)`

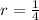
The sum of the first 4 term is 170.

The sum of first n terms of a geometric sequence is given b;

`s_n=(a_1(1-r^n))/(1-r)`

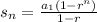
common ratio, n=4 and equate to 170.

`(a_1(1-( (1)/(4) )^4))/(1- (1)/(4) ) = 170`

`(a_1(1- (1)/(256) ))/( (3)/(4) ) = 170\\\\ (255)/(256) a_1 = (3)/(4) * 170\\\\(255)/(256) a_1 = (255)/(2) \\\\(1)/(256) a_1 = (1)/(2) \\\\ a_1 = (1)/(2) * 256\\\\a_1 = (1)/(2) * 256 \\\\= 128`