Question

Suzanne observes two light pulses to be emitted from the same location, but separated in time by 3.00 μs. Mark sees the emission of the same two pulses separated in time by 9.00 μs. (a) How fast is Mark moving relative to Suzanne? (b) According to Mark, what is the separation in space of the two pulses?

Answer 1

Given that,

Separated in time t = 3.00 μs

Separated in time t' = 9.00 μs

(a). We need to calculate the speed

Using formula of time dilation

`t'=\frac{t}{\sqrt{1-(v^2)/(c^2)}}`

`(t)/(t')=\sqrt{1-(v^2)/(c^2)}`

`(v^2)/(c^2)=1-(t^2)/(t'^2)`

`v=c\sqrt{1-(t^2)/(t^2)}`

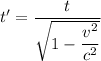
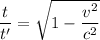
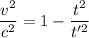
Put the value into the formula

`v=c\sqrt{1-(3.00^2)/(9.00^2)}`

`v=0.942c`

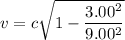
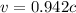
(b). The separation that Mark sees is just the time he sees between the pulse times the speed of light,

Since the first pulse is moving at that speed

We need to calculate the separation in space of the two pulses

Using formula of separation

`x=ct'`

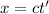
Put the value into the formula

`x=3*10^(8)*9*10^(-6)`

`x=2700\ m`

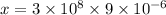
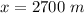
Hence, (a). The speed of mark relative to Suzanne is 0.942c.

(b). The separation in space of the two pulses is 2700 m.