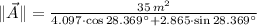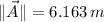Answer:
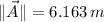
Step-by-step explanation:
Sean A, B y C vectores coplanares tal que:
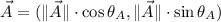 ,
,
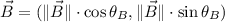 y
y
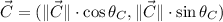
Donde
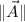 ,
,
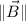 y
y
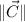 son las normas o magnitudes respectivas de los vectores A, B y C, mientras que
son las normas o magnitudes respectivas de los vectores A, B y C, mientras que
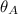 ,
,
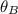 y
y
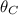 son las direcciones respectivas de aquellos vectores, medidas en grados sexagesimales.
son las direcciones respectivas de aquellos vectores, medidas en grados sexagesimales.
Por definición de producto escalar, se encuentra que:
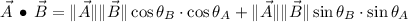
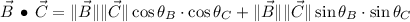
Asimismo, se sabe que
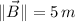 ,
,
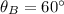 ,
,
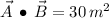 ,
,
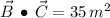 ,
,
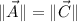 y
y
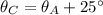 . Entonces, las ecuaciones quedan simplificadas como siguen:
. Entonces, las ecuaciones quedan simplificadas como siguen:
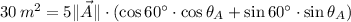
![35\,m^(2) = 5\|\vec A \| \cdot [\cos 60^(\circ)\cdot \cos (\theta_(A)+25^(\circ)) + \sin 60^(\circ)\cdot \sin (\theta_(A)+25^(\circ))]](https://img.qammunity.org/2021/formulas/engineering/college/rwawr0sc1bh7mbrj8nc0ytytwhymn8r4j7.png)
Es decir,
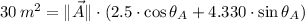
![35\,m^(2) = \| \vec A \| \cdot [2.5\cdot \cos (\theta_(A)+25^(\circ))+4.330\cdot \sin (\theta_(A)+25^(\circ)})]](https://img.qammunity.org/2021/formulas/engineering/college/5vyg2o2ew2qa8nsabrm3o4jicnbzovwt5e.png)
Luego, se aplica las siguientes identidades trigonométricas para sumas de ángulos:
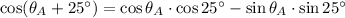
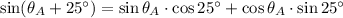
Es decir,
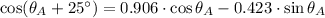
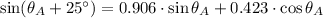
Las nuevas expresiones son las siguientes:
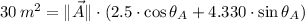
![35\,m^(2) = \| \vec A \| \cdot [2.5\cdot (0.906\cdot \cos \theta_(A) - 0.423 \cdot \sin \theta_(A))+4.330\cdot (0.906\cdot \sin \theta_(A) + 0.423 \cdot \cos \theta_(A))]](https://img.qammunity.org/2021/formulas/engineering/college/ngcyj5blmuf89dgr4tcgtetekt34sh3bm8.png)
Ahora se simplifican las expresiones, se elimina la norma de
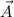 y se desarrolla y simplifica la ecuación resultante:
y se desarrolla y simplifica la ecuación resultante:
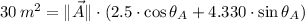
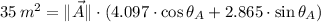
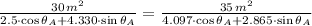
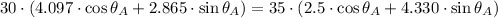
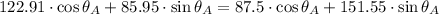
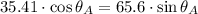
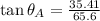
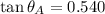
Ahora se determina el ángulo de
 :
:
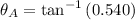
La función tangente es positiva en el primer y tercer cuadrantes y tiene un periodicidad de 180 grados, entonces existen al menos dos soluciones del ángulo citado:
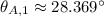 y
y
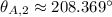
Ahora, la magnitud de
 es:
es: