Question

A highway engineer knows that his crew can lay 5 miles of highway on a clear day, 2 miles on a rainy day, and only 1 mile on a snowy day. Suppose the probabilities are as follows: A clear day: .6, a rainy day: .3, a snowy day: .1. What are the mean and variance

Answer 1

Mean = 3.7

Variance = 2.61

Explanation:

From the data given; we can represent our table into table format for easier solution and better understanding.

Given that:

A highway engineer knows that his crew can lay 5 miles of highway on a clear day, 2 miles on a rainy day, and only 1 mile on a snowy day

Let X represent the crew;

P(X) represent their respective probabilities

clear day rainy day snowy day

X 5 2 1

P(X) 0.6 0.3 0.1

From Above; we can determine our X*P(X) and X²P(X)

Let have the two additional columns to table ; we have

X P(X) X*P(X) X²P(X)

5 0.6 3 15

2 0.3 0.6 1.2

1 0.1 0.1 0.1

Total 1.0 3.7 16.3

The mean
`\mu` can be calculated by using the formula:

`\sum \limits ^n _(i=1)X_i P(X_i)`

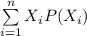
Therefore ; mean
`\mu` = 3.7

Variance
`\sigma^2 = \sum \limits ^n _(i=1)X^2_i P(X_i)- \mu^2`

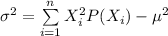
Variance = 16.3 -3.7²

Variance = 16.3 - 13.69

Variance = 2.61