Question

Sally holds an investment with an interest rate of 12.3% compounded annually.

How many years will it take for her investment to triple in value?


7

9

13

6

4

Answer 1

No. of years it will take for the investment to get tripled:

t ≅ 9 years

Explanation:

Interest rate = 12.3%

The compound interest formula is given by:

`A = P(1+(r)/(n))^(nt)`

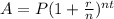
Where

A = Future amount

P = Present amount (Principal amount)

r = Interest rate in decimal form

n = No. of times compounded per year

t = time in years.

We can say that if:

Present amount = P

Future amount = 3P

r = 12.3/100 = 0.123

n = 1

t = ?

Substitute the values in the formula of compound interest:

`3P = P(1+(0.123)/(1))^(1t)\\3P=P(1.123)^t \\3=(1.123)^t\\`

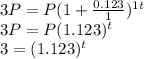
Taking log on both sides.

`log (3)=log(1.123)^t\\log(3)=t\cdot{log(1.123)}\\t=(log(3))/(log(1.123))\\t=9.47`

Round off to nearest option

t ≅ 9 years