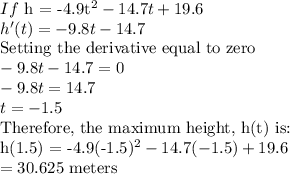Question

A water balloon is thrown from the top of a house. The path of the balloon is modelled by the relation, h = -4.9t2 – 14.7t + 19.6,

where h is the balloon's height, in meters, above ground, and wheret is the time, in seconds.
a.
How tall is the house? (1 mark)
b. How long does it take for the balloon to hit the ground? (3 marks)
What is the maximum height that the balloon reaches? marks)
C.​

Answer 1

(a)19.6 meters

(b) 1 seconds

(c)30.625 meters

Explanation:

The height of the balloon is modeled by the equation:

`h = -4.9t^2- 14.7t + 19.6`

(a)Since the balloon is thrown from the top of the house, the height of the house is at t=0

When t=0

`h(0) = -4.9(0)^2- 14.7(0) + 19.6\\h=19.6$ meters`

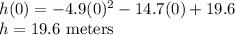
The height of the house is 19.6 meters.

(b)When the balloon hits the ground

Its height, h(t)=0

Therefore, we solve h(t)=0 for values of t.

`h = -4.9t^2- 14.7t + 19.6=0`

`-49t^2-147t+196=0\\-49(t^2+3t-4)=0\\t^2+4t-t-4=0\\t(t+4)-1(t+4)=0\\(t+4)(t-1)=0\\t+4=0$ or $t-1=0\\t=-4$ or t=1`

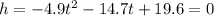
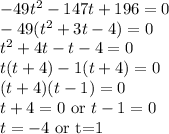
Therefore, the ball hits the ground after 1 seconds.

(c)To determine the maximum height, we take the derivative of the function and solve it for its critical point.

`If$ h = -4.9t^2- 14.7t + 19.6\\h'(t)=-9.8t-14.7\\$Setting the derivative equal to zero$\\-9.8t-14.7=0\\-9.8t=14.7\\t=-1.5\\$Therefore, the maximum height, h(t) is:\\h(1.5) = -4.9(-1.5)^2- 14.7(-1.5) + 19.6\\=30.625$ meters`