Answer:
Explanation:
We are given the equation
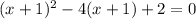 . Consider the substitution u = (x+1). Then the equation turns out to be
. Consider the substitution u = (x+1). Then the equation turns out to be
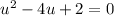
Recall that given a second degree polynomial of the form
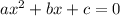 then its solutions are given by the expression
then its solutions are given by the expression
![x = \frac{-b \pm \sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2021/formulas/mathematics/high-school/blzih2n4birlry74b98s5wt2blugjf58n4.png)
In our case, a = 1, b = -4 and c =2. Then the solutions are
![u_1 = \frac{4+\sqrt[]{(-4)^2-4(2)}}{2} = 2 +\sqrt[]{2}](https://img.qammunity.org/2021/formulas/mathematics/college/m5vedkvgalsfge9ohml4rd1hpum81phexj.png)
![u_2 = \frac{4-\sqrt[]{(-4)^2-4(2)}}{2} = 2 -\sqrt[]{2}](https://img.qammunity.org/2021/formulas/mathematics/college/b6phc5zdqlrla14oianqcpy8vyqhwrwdk8.png)
We have that x = u-1. So the original solutions are
![x_1 = 2 +\sqrt[]{2}-1 = 1 + \sqrt[]{2}](https://img.qammunity.org/2021/formulas/mathematics/college/xkpfnf0lsrpbxp5lkihc1rxs7zpjy26ysn.png)
![x_2 =2 -\sqrt[]{2} -1 = 1 - \sqrt[]{2}](https://img.qammunity.org/2021/formulas/mathematics/college/95mvuicidfpg9lvxc5aw9lku58j8oirrxc.png)