Question

Type the correct answer in each box. If necessary, use /for the fraction bars

Answer 1

The experimental probability of rolling an odd number is 60%, which is 10% more than the theoretical probability.

Explanation:

The complete question is:

Type the correct answer in each box. Use numerals instead of words. If necessary, use/ for the fraction bar(s).

A special 8-sided die is marked with the numbers 1 to 8. It is rolled 20 times with these outcomes.

3, 4, 5, 2, 7, 1, 3, 7, 2, 6, 2, 1, 7, 3, 6, 1, 8, 3, 5, 6

The experimental probability of rolling an odd number is _%, which is _% more than the theoretical probability.

Solution:

The possible outcomes of rolling an 8-sided die are:

S = {1, 2, 3, 4, 5, 6, 7, 8}

The odd numbers are:

Odd = {1, 3, 5, 7} = 4 outcomes

The theoretical probability of rolling an odd number is:

`P_(T)(\text{Odd})=\farc{4}{8}=(1)/(2)=50\%`

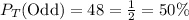
Now from the given 20 outcomes the odd values are:

Odd = {3, 5, 7, 1, 3, 7, 1, 7, 3, 1, 3, 5} = 12 outcomes

Compute the experimental probability of rolling an odd number as follows:

`P_(E)(\text{Odd})=(12)/(20)=(3)/(5)=60\%`

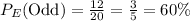
Thus, the experimental probability of rolling an odd number is 60%, which is 10% more than the theoretical probability.