Question

The U.S. Commission on Crime randomly selects 600 files of recently committed crimes in an area and finds 380 in which a firearm was reportedly used. Find a 95% confidence interval for p, the true fraction of crimes in the area in which some type of firearm was reportedly used.

Answer 1

95% confidence interval for p, the true fraction of crimes in the area in which some type of firearm was reportedly used.

(0.59445 , 0.67155)

Explanation:

Explanation:-

Given random sample size 'n' = 600

sample proportion

`p^(-) = (x)/(n) = (380)/(600) = 0.633`

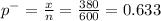
95% of confidence interval for Population proportion is determined by

`(p^(-) - Z_{(\alpha )/(2) } \sqrt{(p^(-) (1-p^(-) ))/(n) } , p^(-) +Z_{(\alpha )/(2) } \sqrt{(p^(-) (1-p^(-) ))/(n) })`

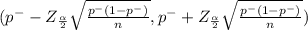
Level of significance : α = 0.05

`z_{(0.05)/(2) } = Z_(0.025) =1.96`

`(0.633 - 1.96 \sqrt{(0.633 (1-0.633 ))/(600 )}, (0.633 + 1.96 \sqrt{(0.633 (1-0.633 ))/(600 )`

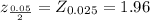
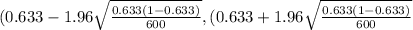
On calculation , we get

(0.633 - 0.03855 , (0.633 + 0.03855)

(0.59445 , 0.67155)

Conclusion:-

95% confidence interval for p, the true fraction of crimes in the area in which some type of firearm was reportedly used.

(0.59445 , 0.67155)