Answer:
The first sequence has a common ratio of 2 while the second sequence has a common ratio of 4.
Explanation:
Given the two sequences
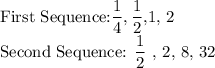
By observation:
In the first sequence:

In the second sequence
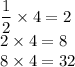
We can see that both sequences are geometric sequences.
However, the first sequence has a common ratio of 2 while the second sequence has a common ratio of 4.