Answer:
Explanation:
The objective is to Show that if the set of images {T(v1)......T(vp)} is linearly dependent, then {v1......vp} is linearly dependent.
Given that:
![\mathbf{[T(v_1) +T(v_2) ...T(v_p)]}](https://img.qammunity.org/2021/formulas/mathematics/college/o9zk0z902zuzrao4nv5mi3cefez1s3ybsj.png) is linearly dependent set
is linearly dependent set
Thus; there exists scalars
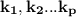 ; ( read as "such that")
; ( read as "such that")
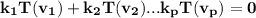
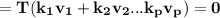
T = 0 (for the fact that T is linear transformation)
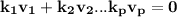 (due to T is one-one)
(due to T is one-one)
NOTE: Not all Ki's are zero;
Thus;
![\mathbf{[v_1,v_2 ...v_p] }](https://img.qammunity.org/2021/formulas/mathematics/college/et86vf9vey9upiiglzmkg6soy92mkpe8pb.png) is linearly dependent
is linearly dependent
It negation also illustrates that :
If
![\mathbf{[v_1,v_2 ...v_p]}](https://img.qammunity.org/2021/formulas/mathematics/college/tpyxlt0ky1lnzmxhcwvgfkcbk6qotxwmpq.png) is also linearly independent then
is also linearly independent then
![\mathbf{[T(v_1),T(v_2) ...T(v_p)]}](https://img.qammunity.org/2021/formulas/mathematics/college/n1p1sur6gntky65eu94px7kewu2haub509.png) is also linearly independent.
is also linearly independent.