Question

The longest side of an acute triangle measures 30 inches. The two remaining sides are congruent, but their length is

unknown

What is the smallest possible perimeter of the triangle, rounded to the nearest tenth?

41.0 in

512 in

724 in

81.2 in

Answer 1

(C)72.4 in

Explanation:

Given an acute triangle in which the longest side measures 30 inches; and the other two sides are congruent.

Consider the attached diagram

AB=BC=x

However to be able to solve for x, we form a right triangle with endpoints A and C.

Since the hypotenuse is always the longest side in a right triangle

Hypotenuse, AC=30 Inches

Using Pythagoras Theorem

`30^2=x^2+x^2\\900=2x^2\\x^2=450\\x=√(450)\\x=21.21$ inches`

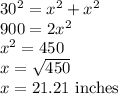
Therefore, the smallest possible perimeter of the triangle

Perimeter=2x+30

=2(21.21)+30

=42.42+30

=72.4 Inches (rounded to the nearest tenth)