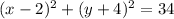Question

The points J(-1,-9) and K(5,1) are endpoints of a diameter of circle S. Which equation represents circle S? A. (x − 2)2 + (y + 4)2 = 34 B. (x − 2)2 + (y + 4)2 = 136 C. (x + 2)2 + (y − 4)2 = 34 D. (x + 2)2 + (y − 4)2 = 136

Answer 1

the equation of the circle is

`(x-2)^2+(y+4)^2 = 34`

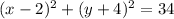
Explanation:

Recall that the equation of a circle is given by
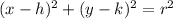`(x-h)^2+(y-k)^2 = r^2` where r is the radius, and (h,k) is the center. Recall that given two points that are the endpoints of a diameter, the center of the circle is their correspondent midpoint. Also, recall that given points (a,b), (c,d) their midpoint is obtained by
`((a+c)/(2),(b+d)/(2))`

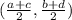
In this case we are given the endpoints (-1,-9), (5,1). So the center of the circle is the midpoint obtained by
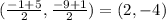`((-1+5)/(2),(-9+1)/(2)) = (2, -4)`. Recall that the radius of a circle is the distance from the radius to any of the points of the circle. So, the radius is the distance between the center and the point (-1,-9). We will calculate r^2, by using the distance formula. REcall that the distance between points (a,b), (c,d) is given by

`\sqrt[]{(a-c)^2+(b-d)^2}`. So, its square is

`(a-c)^2+(b-d)^2`.

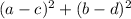In our case,

`r^2 = (2-(-1))^2+(-4-(-9))^2 = 3^2+5^2 = 34`

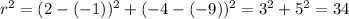
So, the equation of the circle is

`(x-2)^2+(y+4)^2 = 34`