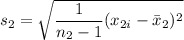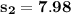Question

Many smartphones, especially those of the LTE-enabled persuasion, have earned a bad rap for exceptionally bad battery life. Battery life between charges for the Motorola Droid Razr Max averages 20 hours when the primary use is talk time and 7 hours when the Internet applications (The wall Street Journal, March 7, 2012).

Since the mean hours for talk time usage is greater than the mean hours for Internet usage, the question was raised as to whether the variance in hours of usage is also greater when the primary use Sample data showing battery hours of use for the two applications follows:
Primary use talking:
35.8 22.2 4.0 32.6 3.5 42.5
8.0 3.8 30.0 12.8 10.3 35.5
Primary use Internet:
24.0 12.5 36.4 1.9 9.9
5.4 1.0 15.2 4.0 4.7
a. Formulate hypotheses about the two population variances that can be used to determine if the population variance in battery hours of use is greater for the talk time application.
H1:σ21_____
Ha:σ22_____
b. What are the standard deviations of battery hours of use for the two samples? Round your answers to two decimal places.
S1_____
S2_____
c. Conduct the hypothesis test and compute the p-value.
- The value of _____
- P-value is _____

Answer 1

Null hypothesis: the variance in hours of usage for talking is not greater than the the variance in hours of usage for internet.

`H_o`:
`\sigma _1 ^2 \leq \sigma _2^2`

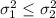
Alternative hypothesis: the variance in hours of usage for talking is greater than the the variance in hours of usage for internet.

`H_a : \sigma_1^2 > \sigma_2^2`

`\mathbf{s_ 1 =16.11}`

`\mathbf{s_2 = 7.98}`

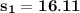
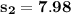
Explanation:

Let
`x_1` and
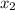`x_2` be the two variables that represents the battery life in hours for talking usage and battery life in hours for internet usage respectively.

The hypothesis can be formulated as:

Null hypothesis: the variance in hours of usage for talking is not greater than the the variance in hours of usage for internet.

`H_o`:
`\sigma _1 ^2 \leq \sigma _2^2`

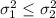
Alternative hypothesis: the variance in hours of usage for talking is greater than the the variance in hours of usage for internet.

`H_a : \sigma_1^2 > \sigma_2^2`

The standard deviation for the battery usage for talking is :

`\bar x_1 = (1)/(n_1) \sum x_i \\ \\ \bar x_1 = (1)/(12)(35.8 +22.4+...+35.5) \\ \\ \bar x_1 = (241.2)/(12) \\ \\ \bar x_1 =20.1`

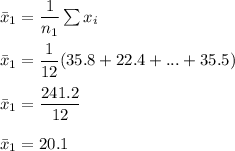
The standard deviation Is:

`s_ 1 = \sqrt{(1)/(n_1-1)\sum (x{_1i}-\bar x_i)^2}`

`s_ 1 = \sqrt{(1)/(12-1)\sum (35.8- 20.1)^2+ (35.5-20.1)^2}`

`s_ 1 = √(259.568)`

`\mathbf{s_ 1 =16.11}`

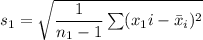
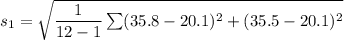
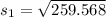
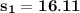
The standard deviation for the battery life usage for the internet is :

`\bar x_2 = (1)/(n_2) \sum x_(2i)`

`\bar x_2 = (1)/(10) (24.0+12.5+36.4+...+4.7})`

`\bar x_2 = (115)/(10)`

`\bar x_2 = 11.5`

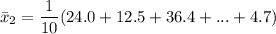
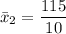
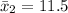
Thus; the standard deviation is:

`s_2 = \sqrt{(1)/(n_2-1)(x_(2i)- \bar x_2)^2}`

`s_2 = \sqrt{(1)/(10-1)(24-11.5)^2+(4.7-11.5)^2}`

`s_2 = √(63.60)`

`\mathbf{s_2 = 7.98}`