Answer:
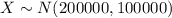
Where
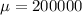 and
and
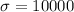
From the empirical rule we know that within one deviation from the mean we have 68% of the values so then 1 deviation above the mean we will have (100-68)/2 = 16% and then the number of houses that are greater than one deviation above the mean are:
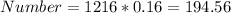
And the answer woud be between 194 and 195 houses
Explanation:
Let X the random variable that represent the value of homes in Hampton VA of a population, and for this case we know the distribution for X is given by:
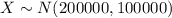
Where
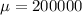 and
and
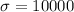
From the empirical rule we know that within one deviation from the mean we have 68% of the values so then 1 deviation above the mean we will have (100-68)/2 = 16% and then the number of houses that are greater than one deviation above the mean are:
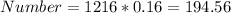
And the answer woud be between 194 and 195 houses