Question

The department of public safety has an old memo stating that the number of accidents per week at a hazardous intersection varies according to a Normal distribution, with a mean of 2.2 and a standard deviation of 1.4. Department officials implemented a new safety plan, heavier police patrols and new signs, to see if they could reduce the average number of accidents at this intersection. They recorded the number of accidents per week for 52 weeks. They find that the average over that period was two accidents per week.

What is the PP‑value for the test of H0:????=2.2 against H????:????<2.2H0:μ=2.2 against Ha:μ<2.2 ?
A. 0.8485
B. 0.4443
C. 0.1515

Answer 1

C. 0.1515

Explanation:

The main objective here is to find the P-value for the test of
`H_0`

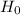
Given that ;

the mean value = 2.2

the standard deviation = 1.4

number of recorded accident per week = 52

The null hypothesis is :
`H_o: \mu =2`

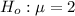
The alternative hypothesis is :
`H_A = \mu < 2`

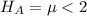
The Z- value can be calculated as:

`z = (x- \mu)/((\sigma )/(√(n)))`

`z = (2- 2.2)/((1.4 )/(√(52)))`

`z = (- 0.2)/((1.4 )/(7.211))`

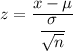
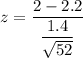
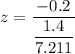
z = -1.03

From the normal distribution table for probability;

P(z< -1.03 ) = 0.1515