Question

A soccer ball is released from rest at the top of a grassy incline. After 8.6 seconds, the ball travels 87 meters and 1.0 s after this, the ball reaches the bottom of the incline. (a) What was the magnitude of the ball's acceleration, assume it to be constant

Answer 1

a) a = 2.35 m/s^2

Step-by-step explanation:

(a) In order to calculate the magnitude of the acceleration of the ball, you use the following formula, for the position of the ball:

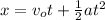`x=v_ot+(1)/(2)at^2` (1)

x: position of the ball after t seconds = 87 m

t: time = 8.6 s

a: acceleration of the ball = ?

vo: initial velocity of the ball = 0 m/s

You solve the equation (1) for a:

`x=0+(1)/(2)at^2\\\\a=(2x)/(t^2)`

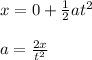
You replace the values of the parameters in the previous equation:

`a=(2(87m))/((8.6s)^2)=2.35(m)/(s^2)`

The acceleration of the ball is 2.35 m/s^2