Answer:
Explanation:
Let P be the population of the community
So the population of a community increase at a rate proportional to the number of people present at a time
That is
![(dp)/(dt) \propto p\\\\(dp)/(dt) =kp\\\\ [k \texttt {is constant}]\\\\(dp)/(dt) -kp =0](https://img.qammunity.org/2021/formulas/mathematics/college/lzts71zli7cro4yo6cypwtjwjr0umhpxk9.png)
Solve this equation we get

where p is the present population
p₀ is the initial population
If the initial population as doubled in 5 years
that is time t = 5 years
We get
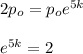
Apply In on both side to get
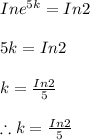
Substitute
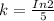 in
in
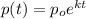 to get
to get
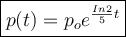
Given that population of a community is 9000 at 3 years
substitute t = 3 in
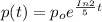
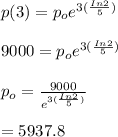
Therefore, the initial population is 5937.8