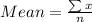Question

Use the data set to answer the question. {22,26,28,35,45,63,91} What is the mean absolute deviation (MAD) of the data set? Enter your answer as a number rounded to the nearest tenth, like this: 42.5

Answer 1

`M.A.D = 18.9`

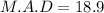
Explanation:

Given: 22,26,28,35,45,63,91

Required: Mean Absolute Deviation

The first step is to solve for the mean of the given data

`Mean = (\sum x)/(n)`

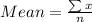
where x->22,26,28,35,45,63,91 and n = 7

`Mean = (22+26+28+35+45+63+91)/(7)\\Mean = (310)/(7)\\Mean = 44.29`

Then; subtract the calculated mean from each data

`22 - 44.29 = -22.29\\26 - 44.29 = -18.29\\28 - 44.29 = -16.29\\35 - 44.29 = -9.29\\45 - 44.29 = 0.71\\63 - 44.29 = 18.71\\91 - 44.29 = 46.71`

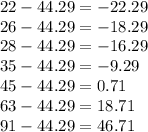
Get Absolute Values of the above results

`|-22.29| = 22.29\\|-18.29| = 18.29 \\|-16.29| = 16.29\\|-9.29| = 9.29\\|0.71| = 0.71\\|18.71| = 18.71\\|46.71|= 46.71`

Calculate the mean of the above result to get the M.A.D

`Mean = (\sum x)/(n)`

`M.A.D = (22.29+18.29+16.29+9.29+0.71+18.71+46.71)/(7)\\M.A.D = (132.29)/(7)\\M.A.D = 18.8985714286\\M.A.D = 18.9`