Question

A University of Florida economist conducted a study of Virginia elementary school lunch menus During the state-mandated testing period, school lunches average 863 calories The economist claims that after the testing period ends, the average caloric content of Virginia school lunches drops significantly They collected a random sample of 500 students' school lunches around Virginia

a). What null and alternative hypotheses should you test?
b). Set up the rejection region for this study using alpha = 0.05 Interpret alpha = 0.05 in the words of the problem
c). Suppose the sample data yielded the test statistic z = -2.17 What conclusion can you draw for the test?
d). Calculate the observed p-value for the test statistic z = -2.17 Interpret the p-value and draw the conclusion based on it

Answer 1

a) Null hypothesis:
`\mu \geq 863`

Alternative hypothesis:
`\mu >863`

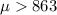
b) For this case using the significance level of
`\alpha=0.05` we can use the normal standard distirbution in order to find a quantile who accumulates 0.05 of the area in the left and we got:

`z_(\alpha)=-1.64`

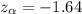
And the rejection zone would be:

`z<-1.64`

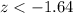
c) For this case since the statistic calculated is lower than the critical value we have enough evidence to reject the null hypothesis at 5% of significance

d)
`p_v = P(z<-2.17) =0.015`

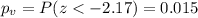
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis at the significance level provided

Explanation:

Part a

We want to test for this case if the true mean is significantly less than 863 calories so then the system of hypothesis are:

Null hypothesis:
`\mu \geq 863`

Alternative hypothesis:
`\mu >863`

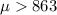
Part b

For this case using the significance level of
`\alpha=0.05` we can use the normal standard distirbution in order to find a quantile who accumulates 0.05 of the area in the left and we got:

`z_(\alpha)=-1.64`

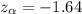
And the rejection zone would be:

`z<-1.64`

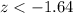
Part c

For this case since the statistic calculated is lower than the critical value we have enough evidence to reject the null hypothesis at 5% of significance

Part d

For this case the p value would be given by:

`p_v = P(z<-2.17) =0.015`

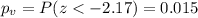
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis at the significance level provided