Answer:
The average rate of change in the balance over the interval t = 0 to t = 5 is of $20.82 a year. This means that the balance increased by $20.82 a year over the interval t = 0 to t = 5.
Explanation:
Given a function y, the average rate of change S of y=f(x) in an interval
 will be given by the following equation:
will be given by the following equation:
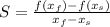
In this problem, we have that:
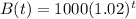
Find the average rate of change in the balance over the interval t = 0 to t = 5.
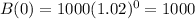
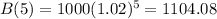
Then
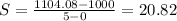
The average rate of change in the balance over the interval t = 0 to t = 5 is of $20.82 a year. This means that the balance increased by $20.82 a year over the interval t = 0 to t = 5.