Question

Random samples of students were compared to see whether or not there was a difference in the proportion favoring the university's proposed switch from MWF (three-day) classes to MW and TR (two-day) classes. In the resident population 80 out of 200 favored the switch. In the commuter population, 120 out of 200 favored the switch. Conduct a hypothesis test at the .05 significance level to see if there is a difference in the proportion of residents and commuters who prefer the switch.

Answer 1

There is enough evidence to support the claim that there is a significant difference in the proportion of residents and commuters who prefer the switch.

Explanation:

This is a hypothesis test for the difference between proportions.

The claim is that there is a significant difference in the proportion of residents and commuters who prefer the switch.

Then, the null and alternative hypothesis are:

`H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2\\eq 0`

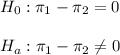
The significance level is 0.05.

The sample 1 (residents), of size n1=200 has a proportion of p1=0.4.

`p_1=X_1/n_1=80/200=0.4`

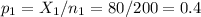
The sample 2 (conmuters), of size n2=200 has a proportion of p2=0.6.

`p_2=X_2/n_2=120/200=0.6`

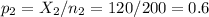
The difference between proportions is (p1-p2)=-0.2.

`p_d=p_1-p_2=0.4-0.6=-0.2`

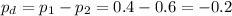
The pooled proportion, needed to calculate the standard error, is:

`p=(X_1+X_2)/(n_1+n_2)=(80+120)/(200+200)=(200)/(400)=0.5`

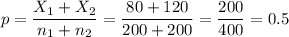
The estimated standard error of the difference between means is computed using the formula:

`s_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.5*0.5)/(200)+(0.5*0.5)/(200)}\\\\\\s_(p1-p2)=√(0.0013+0.0013)=√(0.0025)=0.05`

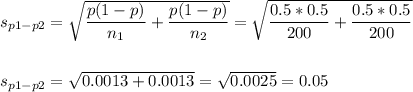
Then, we can calculate the z-statistic as:

`z=(p_d-(\pi_1-\pi_2))/(s_(p1-p2))=(-0.2-0)/(0.05)=(-0.2)/(0.05)=-4`

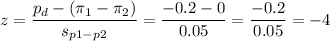
This test is a two-tailed test, so the P-value for this test is calculated as (using a z-table):

`P-value=2\cdot P(z<-4)=0.00008`

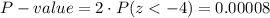
As the P-value (0.00008) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that there is a significant difference in the proportion of residents and commuters who prefer the switch.