Answer:
(a) The probability that a randomly selected athlete uses a stairclimber for less than 19 minutes is 0.2388.
(b) The probability that a randomly selected athlete uses a stairclimber for between 24 and 33 minutes is 0.3997.
(c) The probability that a randomly selected athlete uses a stairclimber for more than 40 minutes is 0.0113.
Step-by-step explanation:
We are given that the amounts of time per workout an athlete uses a stairclimber are normally distributed, with a mean of 24 minutes and a standard deviation of 7 minutes.
Let X = amounts of time per workout an athlete uses a stairclimber
So, X ~ Normal(
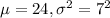 )
)
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean time = 24 minutes
= mean time = 24 minutes
 = standard deviation = 7 minutes
= standard deviation = 7 minutes
(a) The probability that a randomly selected athlete uses a stairclimber for less than 19 minutes is given by P(X < 19 minutes)
P(X < 19 min) = P(
 <
<
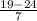 ) = P(Z < -0.71) = 1 - P(Z
) = P(Z < -0.71) = 1 - P(Z
 0.71)
0.71)
= 1 - 0.7612 = 0.2388
The above probability is calculated by looking at the value of x = 0.71 in the z table which has an area of 0.7612.
(b) The probability that a randomly selected athlete uses a stairclimber for between 24 and 33 minutes is given by = P(24 min < X < 33 min)
P(24 min < X < 33 min) = P(X < 33 min) - P(X
 24 min)
24 min)
P(X < 33 min) = P(
 <
<
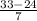 ) = P(Z < 1.28) = 0.8997
) = P(Z < 1.28) = 0.8997
P(X
 24 min) = P(
24 min) = P(


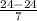 ) = P(Z
) = P(Z
 0) = 0.50
0) = 0.50
The above probability is calculated by looking at the value of x = 1.28 and x = 0 in the z table which has an area of 0.8997 and 0.50 respectively.
Therefore, P(24 min < X < 33 min) = 0.8997 - 0.50 = 0.3997
(c) The probability that a randomly selected athlete uses a stairclimber for more than 40 minutes is given by P(X > 40 minutes)
P(X > 40 min) = P(
 >
>
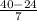 ) = P(Z > 2.28) = 1 - P(Z
) = P(Z > 2.28) = 1 - P(Z
 2.28)
2.28)
= 1 - 0.9887 = 0.0113
The above probability is calculated by looking at the value of x = 2.28 in the z table which has an area of 0.9887.
The event of probability that a randomly selected athlete uses a stairclimber for more than 40 minutes is unusual because this probability is less than 5% and any even whose probability is less than 5% is said to be unusual.