Question

Which statement best describes f (x) = negative 2 StartRoot x minus 7 EndRoot + 1?

–6 is in the domain of f(x) but not in the range of f(x).

–6 is not in the domain of f(x) but is in the range of f(x).

–6 is in the domain of f(x) and in the range of f(x).

–6 is neither in the domain of f(x) nor in the range of f(x).

Answer 1

B

Explanation:

Answer 2

Option B.

Explanation:

The given function is

`f(x)=-2√(x-7)+1`

The above function is defined if (x-7) is greater than 0.

`x-7\geq 0`

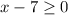
Add 7 on both sides.

`x\geq 7`

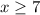
It is means domain of the function is
`[7,\infty)`. So, -6 is not in domain.

We know that

`√(x-7)\geq 0`

Multiply both sides by -2. So, the sign of inequality will change.

`-2√(x-7)\leq 0`

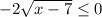
Add 1 on both sides.

`-2√(x-7)+1\leq 0+1`

`f(x)\leq 1`

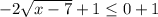
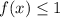
It is means range of the function is
`(-\infty,1]`. So, -6 is in Range.

Since –6 is not in the domain of f(x) but is in the range of f(x), therefore the correct option is B.