Question

A magazine provided results from a poll of 500500 adults who were asked to identify their favorite pie. Among the 500500 ​respondents, 1414​% chose chocolate​ pie, and the margin of error was given as plus or minus±33 percentage points. Given specific sample​ data, which confidence interval is​ wider: the 9999​% confidence interval or the 8080​% confidence​ interval? Why is it​ wider?

Answer 1

99% confidence interval is wider as compared to the 80% confidence interval.

Explanation:

We are given that a magazine provided results from a poll of 500 adults who were asked to identify their favorite pie.

Among the 500 respondents, 14​% chose chocolate​ pie, and the margin of error was given as plus or minus ±3 percentage points.

The pivotal quantity for the confidence interval for the population proportion is given by;

P.Q. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of adults who chose chocolate​ pie = 14%

n = sample of adults = 500

p = true proportion

Now, the 99% confidence interval for p =
`\hat p \pm Z_(_(\alpha)/(2)_) * \sqrt{(\hat p(1-\hat p))/(n) }`

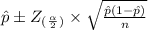
Here,
`\alpha` = 1% so
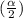`((\alpha)/(2))` = 0.5%. So, the critical value of z at 0.5% significance level is 2.5758.

Also, Margin of error =
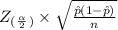`Z_(_(\alpha)/(2)_) * \sqrt{(\hat p(1-\hat p))/(n) }` = 0.03 for 99% interval.

So, 99% confidence interval for p =
`0.14 \pm2.5758 * \sqrt{(0.14(1-0.14))/(500) }`

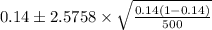
= [0.14 - 0.03 , 0.14 + 0.03]

= [0.11 , 0.17]

Similarly, 80% confidence interval for p =
`0.14 \pm 1.2816 * \sqrt{(0.14(1-0.14))/(500) }`

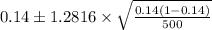
Here,
`\alpha` = 20% so
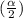`((\alpha)/(2))` = 10%. So, the critical value of z at 10% significance level is 1.2816.

Also, Margin of error =
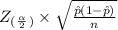`Z_(_(\alpha)/(2)_) * \sqrt{(\hat p(1-\hat p))/(n) }` = 0.02 for 80% interval.

So, 80% confidence interval for p = [0.14 - 0.02 , 0.14 + 0.02]

= [0.12 , 0.16]

Now, as we can clearly see that 99% confidence interval is wider as compared to 80% confidence interval. This is because more the confidence level wider is the confidence interval and we are more confident about true population parameter.