Question

A ball is thrown straight up from the top of a 40 feet tall building with an initial speed of 24 feet per second. The height of the ball as a function of time can be modeled by what function h(t) = _________________ 1. after how many seconds the ball hit the ground. 2.What is the maximum height of the ball? 3.How long did it take for the ball to reach its maximum height?

Answer 1

1)The ball hits the ground after 3 seconds.

2)The maximum height of the ball is 49 feet

3)It takes 1.25 seconds to reach its maximum height

Explanation:

Height of building = 40 feet

We are given that A ball is thrown straight up from the top of building with an initial speed of 24 feet per second.

So, The height of the ball as a function of time can be modeled by:
`h(t)=-16t^2+40t+24`

1)After how many seconds the ball hit the ground.

Substitute h(t)=0

So,
`-16t^2+40t+24=0\\-2t^2+5t+3=0\\2t^2-5t-3=0\\2t^2-6t+t-3=0\\2t(t-3)+1(t-3)=0\\(2t+1)(t-3)=0\\t=(-1)/(2) , 3`

Since time cannot be negative

So,the ball hits the ground after 3 seconds.

2)What is the maximum height of the ball?

It takes maximum height at vertex

Formula :
`t = (-b)/(2a)`

`t=(-40)/(2(-16))=1.25 seconds`

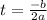
Substitute the value of t in function

`h(1.25)=-16(1.25)^2+40(1.25)+24\\h(1.25)=49 feet`

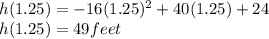
So,the maximum height of the ball is 49 feet

3).How long did it take for the ball to reach its maximum height?

It takes 1.25 seconds to reach its maximum height