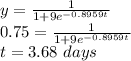Answer:
The answer is shown below
Explanation:
Let y(t) be the fraction of the population that has heard the rumor at time t and assume that the rate at which the rumor spreads is proportional to the product of the fraction y of the population that has heard the rumor and the fraction 1−y that has not yet heard the rumor.
a)
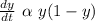
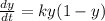
where k is the constant of proportionality, dy/dt = rate at which the rumor spreads
b)

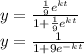
At t = 2, y = 40% = 0.4
c) At y = 75% = 0.75