Answer:
a. pH = 2.52
b. pH = 8.67
c. pH = 12.83
Step-by-step explanation:
The equation of the titration between the benzoic acid and NaOH is:
C₆H₅CO₂H + OH⁻ ⇄ C₆H₅CO₂⁻ + H₂O (1)
a. To find the pH after the addition of 20.0 mL of NaOH we need to find the number of moles of C₆H₅CO₂H and NaOH:

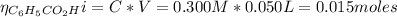
From the reaction between the benzoic acid and NaOH we have the following number of moles of benzoic acid remaining:
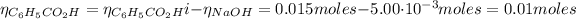
The concentration of benzoic acid is:

Now, from the dissociation equilibrium of benzoic acid we have:
C₆H₅CO₂H + H₂O ⇄ C₆H₅CO₂⁻ + H₃O⁺
0.14 - x x x
![Ka = ([C_(6)H_(5)CO_(2)^(-)][H_(3)O^(+)])/([C_(6)H_(5)CO_(2)H])](https://img.qammunity.org/2021/formulas/chemistry/college/a6v4dhao0z9jyjiidbaq92cpou8kkcqiv3.png)
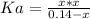
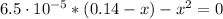 (2)
(2)
By solving equation (2) for x we have:
x = 0.0030 = [C₆H₅CO₂⁻] = [H₃O⁺]
Finally, the pH is:
![pH = -log([H_(3)O^(+)]) = -log (0.0030) = 2.52](https://img.qammunity.org/2021/formulas/chemistry/college/iwbowmf2e2sk6uanvtfl1fsyttcynrts5i.png)
b. At the equivalence point, the benzoic acid has been converted to its conjugate base for the reaction with NaOH so, the equilibrium equation is:
C₆H₅CO₂⁻ + H₂O ⇄ C₆H₅CO₂H + OH⁻ (3)
The number of moles of C₆H₅CO₂⁻ is:
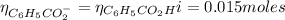
The volume of NaOH added is:

The concentration of C₆H₅CO₂⁻ is:
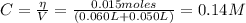
From the equilibrium of equation (3) we have:
C₆H₅CO₂⁻ + H₂O ⇄ C₆H₅CO₂H + OH⁻
0.14 - x x x
![Kb = ([C_(6)H_(5)CO_(2)H][OH^(-)])/([C_(6)H_(5)CO_(2)^(-)])](https://img.qammunity.org/2021/formulas/chemistry/college/h8uw0k0eb46m4tcn78av949laj9hinc4eq.png)
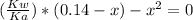

By solving the equation above for x, we have:
x = 4.64x10⁻⁶ = [C₆H₅CO₂H] = [OH⁻]
The pH is:
![pOH = -log[OH^(-)] = -log(4.64 \cdot 10^(-6)) = 5.33](https://img.qammunity.org/2021/formulas/chemistry/college/6x0j22fpqu4f312g3zzc5w844mgktlahpy.png)
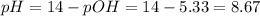
c. To find the pH after the addition of 100 mL of NaOH we need to find the number of moles of NaOH:
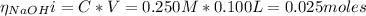
From the reaction between the benzoic acid and NaOH we have the following number of moles remaining:
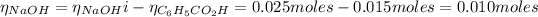
The concentration of NaOH is:
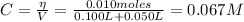
Therefore, the pH is given by this excess of NaOH:
![pOH = -log([OH^(-)]) = -log(0.067) = 1.17](https://img.qammunity.org/2021/formulas/chemistry/college/552udtvvqj2gw5gnqz0cqrfv8nvvqpijgb.png)
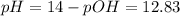
I hope it helps you!