Question

A mail-order computer business has six telephone lines. Let X denote the number of lines in use at a specified time. Suppose the pmf of X is given in the accompanying table

X 0 1 2 3 4 5 6
p(x) .04 .21 .25 .30 .10 .08 .02
Calculate the probability of each of the following events:
(a) At most 4 lines are in use.
(b) Fewer than 2 lines are in use.
(c) At least 3 lines are in use.
2. If k is a constant and X and Y are random variables, then
(i) E(k) = ? (ii) E(kX) = ? (iii) E(X ± Y) = ?

Answer 1

For the probability events:

(a) At most 4 lines in use: P(X <= 4) = 0.90

(b) Fewer than 2 lines in use: P(X < 2) = 0.25

(c) At least 3 lines in use: P(X >= 3) = 0.50

(a) Probability of at most 4 lines in use:

P(X <= 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)

= 0.04 + 0.21 + 0.25 + 0.30 + 0.10

= 0.90

(b) Probability of fewer than 2 lines in use:

P(X < 2) = P(X = 0) + P(X = 1)

= 0.04 + 0.21

= 0.25

(c) Probability of at least 3 lines in use:

P(X >= 3) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)

= 0.30 + 0.10 + 0.08 + 0.02

= 0.50

(2) Expectation (Mean) Properties:

(i) E(k) = k * P(X = k) = k * Σ (all x) x * P(X = x)

(ii) E(kX) = k * E(X) = k * Σ (all x) x * P(X = x)

(iii) E(X ± Y) = E(X) ± E(Y) = Σ (all x) x * P(X = x) ± Σ (all y) y * P(Y = y)

These formulas provide the expected values of random variables based on their probability mass functions.

Answer 2

a. 0.9

b. 0.25

c. 0.5

i. k

ii. k..E( X )

iii. E ( X ) ± E ( Y )

Explanation:

Solution:-

- The probability distribution of a random variable X that denotes the number of lines used in a period of time t. The probability mass function of the RV X is given below:

X 0 1 2 3 4 5 6

p ( X ) 0.04 0.21 0.25 0.30 0.1 0.08 0.02

- We are to calculate the following probabilities:

a) At most four lines are in use.

- Translate the required probability in mathematical expression as follows:

p ( X ≤ 4 ) = p ( X = 0 ) + p ( X = 1 ) + p ( X = 2 ) + p ( X = 3 ) + p ( X = 4 )

- Use the given pmf for the random variable X and determine the required probability as follows:

p ( X ≤ 4 ) = 0.04 + 0.21 + 0.25 + 0.3 + 0.1

p ( X ≤ 4 ) = 0.9 ... Answer

b) Fewer than two lines are in use.

- Translate the required probability in mathematical expression as follows:

p ( X < 2 ) = p ( X = 0 ) + p ( X = 1 )

- Use the given pmf for the random variable X and determine the required probability as follows:

p ( X < 2 ) = 0.04 + 0.21

p ( X < 2 ) = 0.25 ... Answer

c) At least three lines are in use.

- Translate the required probability in mathematical expression as follows:

p ( X ≥ 3 ) = p ( X = 3 ) + p ( X = 4 ) + p ( X = 5 ) + p ( X = 6 )

- Use the given pmf for the random variable X and determine the required probability as follows:

p ( X ≥ 3 ) = 0.3 + 0.1 +0.08 + 0.02

p ( X ≥ 3 ) = 0.5 ... Answer

2. The following properties of the expected value of random variables are as follows:

E ( k ) = k ... provided k is a constant for all iterative values

E ( k.X ) = ∑
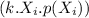`( k.X_i.p( X_i ) )` = k*∑
`( X_i.p( X_i ) )` = k. E ( X )

- For two random variables X and Y the arithmetic expected value is defined as:

E ( X ± Y ) = E ( X ) ± E ( Y ) ... only if both E ( X ) and E ( Y ) exist.