Question

The equation r(t) = sin(6t) i + cos(6t) j, t > 0 describes the motion of a particle moving along the unit circle.

Answer the following questions about the behavior of the particle.
1. Does the particle have constant speed? what is its constant speed?
2. Is the particle's acceleration vector always orthogonal to its velocity vector?
3. Does the particle move clockwise or anticlockwise around the circle?
4. Does the particle begin at the point (1,0)?
5. Select the correct choice ?
(A)The particle's speed is constant.
(B)The particle's speed is not constant.
6. Is the particle's acceleration vector always orthogonal to its velocity vector?
(A) Yes
(B) No
7. Does the particle move clockwise or anticlockwise around the circle?

Answer 1

1. constant speed of 6 units per second

2. yes

3. clockwise

4. no it begins from the point ( 0 , 1 )

Explanation:

Solution:-

- The position of a particle moving in a path of a unit circle is defined by the following vector equation:-

r ( t ) = sin ( 6t ) i + cos ( 6t ) j

- To determine the speed of the particle in the circular motion we will derivate the position vector ( r ) of the particle with respect to time ( t ) to get the velocity vector:

d r (t ) / dt = v ( t )

v ( t ) = 6*[ cos ( 6t ) i - sin ( 6t ) j ]

- We will determine the speed of the particle by determining the magnitude of the velocity vector v ( t ) as follows:

| v(t) | =
`√(6^2 * cos^2 ( 6t ) + 6^2 * sin^2 ( 6t ))`

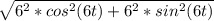
| v(t) | =
`√(36. [cos^2 ( 6t ) + sin^2 ( 6t ) ] )`

| v(t) | =
`√(36.) √(1) = 6`

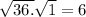
- The speed | v(t) | remians constant at 6 units per second.

- To determine the acceleration vector a ( t ) we will derivate the velocity vector v ( t ) with respect to time t as follows

d v(t) / dt = a ( t )

a ( t ) = - 36 * [ sin ( 6t ) i + cos ( 6t ) j ]

- To determine whether the two vectors v ( t ) and a ( t ) are orthogonal to each other we will apply the dot product test for orthogonal vectors to be equal to zero as follows:

v(t) . a (t) = -6*36 [ cos ( 6t ) * sin ( 6t ) - sin ( 6t ) * cos ( 6t ) ]

v(t) . a (t) = -6*36 [ 0 ] = 0 ... ( proven )

- The velocity and acceleration vectors are orthogonal at all times t.

- To determine the direction of particle motion we will plug in two consecutive values of t = 0 and t = π / 6 and determine the value of position vector r ( t ):

r ( 0 ) = sin ( 0 ) i + cos ( 0 ) j

r ( 0 ) = 0 i + 1 j

r ( π / 12 ) = sin ( π/2 ) i + cos ( π /2 ) j

r ( π / 12 ) = 1 i + 0 j

- Plot the two points r ( 0 ) and r ( π / 12 ) on a Cartesian coordinate system and join the two with a curve directed from [ 0 i + 1 j ] to [ 1 i + 0 j ]. We see the motion is clockwise and starts from point ( 0 , 1 ) not ( 1 , 0 )