Question

A drug is administered intravenously at a constant rate of r mg/hour and is excreted at a rate proportional to the quantity present, with constant of proportionality k>0.

(Set up and) Solve a differential equation for the quantity, Q, in milligrams, of the drug in the body at time t hours. Assume there is no drug in the body initially. Your answer will contain r and k.
Q = _______
Graph Q against t. What is Q?, the limiting long-run value of Q?
Q?= _______
If r is doubled (to 2r), by what multiplicative factor is Q? increased?
Q? (for 2r) = ______ Q? (for r)
Similarly, if r is doubled (to 2r), by what multiplicative factor is the time it takes to reach half the limiting value, 12Q?, changed?
t (to 12Q?), for 2r) =________ t (to 12Q?), for r)
If k is doubled (that is, we use 2k instead of k), by what multiplicative factor is Q? increased?
Q? (for 2k) = _______ Q? (for k)
On the time to reach 12Q??
t (to 12Q?), for 2k) = _____ t (to 12Q?), for k)

Answer 1

See explanation

Explanation:

Solution:-

- We are told that a drug is administered to a patient at a rate of ( r ). The drug present in the patient at time t is Q. The drug also leaves the patient's body at a rate proportional to the amount of drug present at time t.

- We will set up the first order ODE for the rate of change of drug ( Q ) in the patient's body.

`(dQ)/(dt) = ( in-flow ) - ( out-flow )`

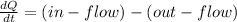
- We know that the rate of inflow is the rate at which the drug is administered that is ( r ) and the flow out is proportional to the amount currently present in the patient's body ( k*Q ). Where ( k ) is the constant of proportionality:

`(dQ)/(dt) = ( r ) - ( k.Q )`

- Express the ODE in the standard form:

`(dQ)/(dt) + k*Q = r`

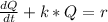
- The integrating factor ( u ) for the above ODE would be:

`u = e^\int^ {k} \, ^d^t = e^(^k^t^)`

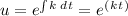
- Use the standard solution of ( Q ) using the integrating factor ( u ):

`u*Q =\int {u.r} \, dt + c\\\\e^(^k^t^)*Q =\int {e^(^k^t^).r} \, dt + c\\\\e^(^k^t^)*Q =(r)/(k)*e^(^k^t^) + c\\\\Q = (r)/(k) + c*e^(^-^k^t^)`

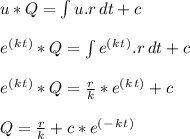
Where, c: the constant of integration.

- The initial value problem is such that there is no drug in the patient body initially. Hence, Q ( 0 ) = 0:

`Q = (r)/(k) + c*(1) = 0\\\\c = -(r)/(k)`

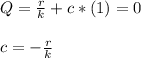
- The solution to the ODE is:

`Q(t) = (r)/(k)* [ 1 - e^(^-^k^t^) ]` .... Answer

- We can use any graphing calculator to plot the amount of drug ( Q ) in the patient body. The limiting value of the drug in the long-run ( t -> ∞ ) can be determined as follows:

Lim ( t -> ∞ ) [ Q ( t ) ] = Lim ( t -> ∞ ) [
`(r)/(k)* [ 1 - (1)/(e^(^-^k^*^i^n^f^) ) ]`

Lim ( t -> ∞ ) [ Q ( t ) ] =
`(r)/(k)* [ 1 - 0 ] = (r)/(k)`

- The long-run limiting value of drug in the body would be ( r / k ).

- If the rate of drug administrative rate is doubled then the amount of ( Q ) at any time t would be:

`Q = (2*r)/(k) * [ 1 - e^(^-^k^t^) ]`

- The multiplicative factor is 2.

- To reach half the limiting value ( 0.5* r / k ) the amount of time taken for the double rate ( 2r ) of administration of drug would be:

`Q = (2*r)/(k) * [ 1 - e^(^-^k^t^) ] = (r)/(2*k) \\\\1 - e^(^-^k^t^) = (1)/(4) \\\\e^(^-^k^t^) = (3)/(4) \\\\kt = - Ln [ 0.75 ]\\\\t = (- Ln [ 0.75 ])/(k)`

- Similarly for the normal administration rate ( r ):

`Q = (r)/(k)* [ 1 - e^(^-^k^t^) ] = (r)/(2k) \\\\1 - e^(^-^k^t^) = (1)/(2) \\\\e^(^-^k^t^) = (1)/(2) \\\\kt = - Ln ( 0.5 ) \\\\t = ( - Ln( 0.5 ))/(k)`

- The multiplicative factor ( M ) of time taken to reach half the limiting value is as follows:

`M = ((-Ln(0.75))/(k) )/((-Ln(0.5))/(k) ) = \frac{Ln ( 0.75 )} { Ln ( 0.5 ) }`

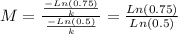
- Similarly repeat the above calculation when the proportionality constant ( k ) is doubled.