Question

Find the range of p in equation p(x+1) (x-3)=x-4p-2 has no real roots. ​

Answer 1

`\displaystyle p > (1)/(4)`.

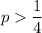Explanation:

Expand the left-hand side of this equation:

`p\, (x + 1)\, (x - 3) = p\, \left(x^2 - 2\, x - 3\right) = p\, x^2 - 2\, p\, x - 3\, p`.

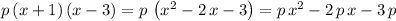Collect the terms, so that this quadratic equation is in the form
`a\, x^2 + b\, x+ c = 0`:

`p\, x^2 - 2\, p\, x - 3\, p = x - 4\, p - 2`.

`p\, x^2 - (2\, p + 1)\, x + (p + 2) = 0`.

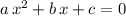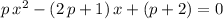In this equation:

• 
  `a = p`.
• 
  `b = -(2\, p + 1)`.
• 
  `c = p + 2`.

Calculate the quadratic discriminant of this quadratic equation:

`\begin{aligned}b^2 - 4\, a\, c &= (-(2\, p + 1))^2 - 4\, p\, (p + 2) \\ &= 4\, p^2 + 4\, p + 1 - 4\, p^2- 8\, p = -4\, p + 1\end{aligned}`.

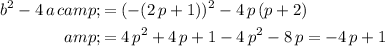A quadratic equation has no real root if its quadratic discriminant is less then zero. As a result, this quadratic equation will have no real root when
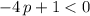`-4\, p + 1 < 0`. Solve for the range of
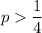`p`:

`\displaystyle p > (1)/(4)`.